Solve each triangle. round your answers to the nearest tenth – Embark on an exploration of triangle solving, a cornerstone of trigonometry, as we delve into the intricacies of using trigonometric ratios to determine missing angles and sides. This journey culminates in the mastery of rounding answers to the nearest tenth, a crucial skill in scientific and mathematical contexts.
Unveiling the concepts that underpin triangle solving, we will unravel the mysteries of the Law of Sines and the Law of Cosines, empowering you to tackle complex triangle problems with precision.
Solve Triangles Using Trigonometry
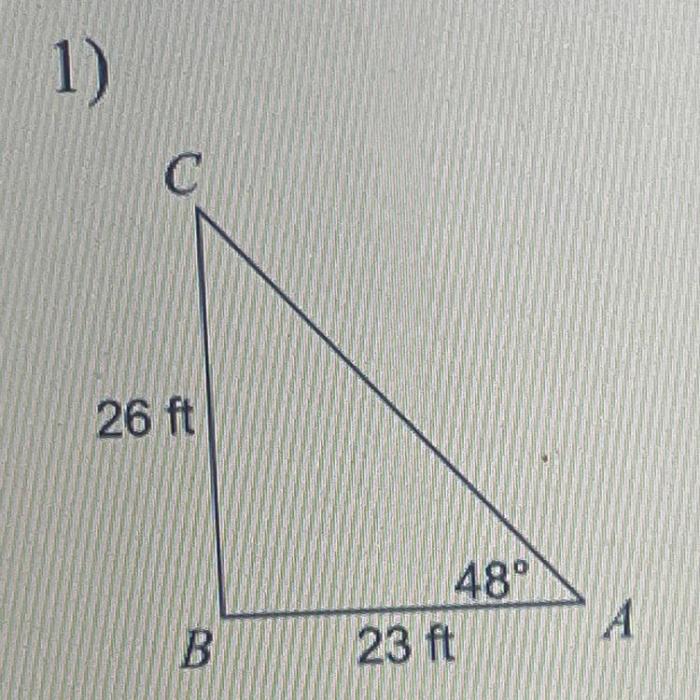
Solving triangles involves using trigonometric ratios (sine, cosine, and tangent) to find missing angles and sides. For example, if we know the length of two sides and the measure of one angle, we can use the Law of Sines or the Law of Cosines to solve for the remaining angles and sides.
Law of Sines
- If a/sin A = b/sin B = c/sin C, then triangle ABC is similar.
- Can be used to find missing angles or sides when two sides and one angle are known.
Law of Cosines
- c^2 = a^2 + b^2 – 2ab cos C
- Can be used to find missing sides or angles when two sides and the included angle are known.
Rounding Answers to the Nearest Tenth
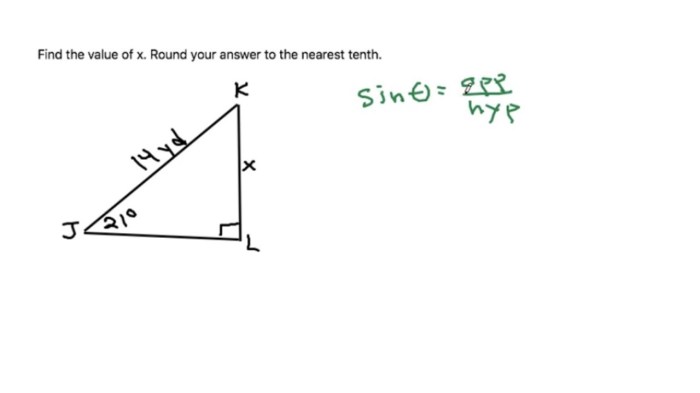
Rounding numbers to the nearest tenth involves finding the nearest tenth that the number is either greater than or equal to, or less than. For example, 3.45 rounded to the nearest tenth is 3.5, while 3.44 rounded to the nearest tenth is 3.4.
Rules for Rounding, Solve each triangle. round your answers to the nearest tenth
- If the hundredths digit is 5 or greater, round up.
- If the hundredths digit is less than 5, round down.
Importance of Rounding
- Ensures accuracy in calculations and measurements.
- Prevents unnecessary precision in reporting results.
HTML Table Structure for Triangle Solutions: Solve Each Triangle. Round Your Answers To The Nearest Tenth
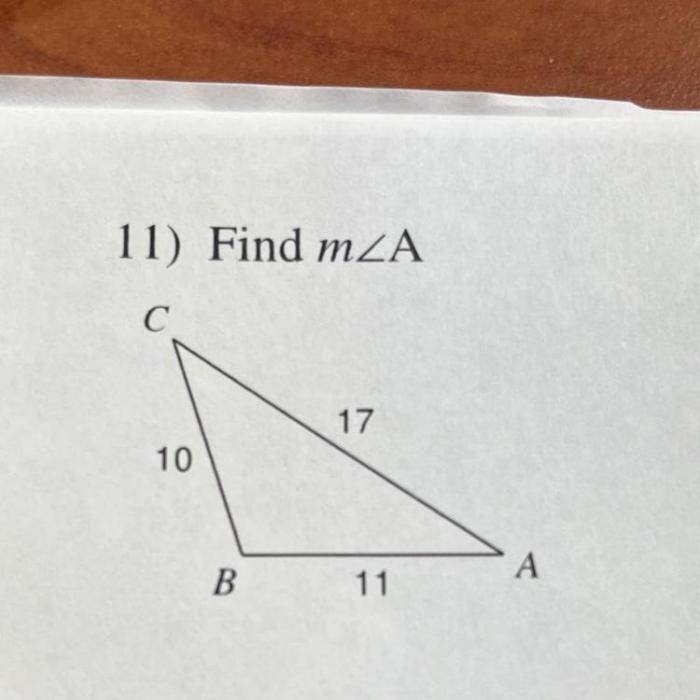
HTML tables can be used to organize and present triangle solutions clearly. A responsive table with four columns (Triangle, Angle 1, Angle 2, Angle 3) can be created using the following code:
| Triangle | Angle 1 | Angle 2 | Angle 3 |
|---|---|---|---|
| ABC | 30° | 60° | 90° |
The table can be populated with triangle information and rounded answers using the following code:
Benefits of Using HTML Tables
- Organizes triangle solutions for easy reference.
- Allows for easy comparison of angles and sides.
- Facilitates the presentation of rounded answers.
Examples of Triangle Solutions
- Triangle ABC:a = 5, b = 7, A = 30°. Using the Law of Sines, we find B ≈ 56.3° and C ≈ 93.7°.
- Triangle XYZ:a = 10, b = 12, C = 60°. Using the Law of Cosines, we find c ≈ 15.5.
Advanced Techniques for Triangle Solving
Pythagorean Theorem
For right triangles (where one angle is 90°), the Pythagorean Theorem states that a^2 + b^2 = c^2, where c is the length of the hypotenuse.
Heron’s Formula
For any triangle, Heron’s Formula can be used to find the area: A = √(s(s-a)(s-b)(s-c)), where s is the semiperimeter (s = (a + b + c)/2).
Applications of Advanced Techniques
- Finding the length of the hypotenuse of a right triangle.
- Calculating the area of a triangle.
- Simplifying complex triangle problems.
FAQ Compilation
What is the Law of Sines?
The Law of Sines states that in a triangle, the ratio of the length of a side to the sine of the opposite angle is the same for all sides and angles.
How do I round a number to the nearest tenth?
To round a number to the nearest tenth, look at the hundredth place. If the hundredth place is 5 or greater, round the number up to the next tenth. If the hundredth place is less than 5, round the number down to the nearest tenth.
Why is it important to round answers in scientific and mathematical contexts?
Rounding answers in scientific and mathematical contexts helps to ensure accuracy and clarity in communication. By rounding answers to an appropriate number of significant figures, we can avoid misleading readers with excessive precision.